A Cocoa implementation of CONREC

Generate contours and convert to vector/bezier form [Download demo source code - 38K Xcode project ]

CONREC is a popular algorithm used for generating contour lines from three-dimensional height data. While more sophisticated algorithms certainly exist, for many uses CONREC is perfectly adequate, and has the advantage of being easy to understand and implement, reasonably fast, and well-known in the public domain. It was written by Paul Bourke in the mid 1980s, and published in BYTE Magazine in 1987. The article with accompanying explanations, diagrams and generic code is available at the following link (Objective-C code that encapsulates the CONREC algorithm in a useful class for Cocoa developers is given below).

http://local.wasp.uwa.edu.au/~pbourke/papers/conrec/

CONREC in Cocoa

CONREC has been ported to many languages including C but its utility for Cocoa programmers can be usefully improved by wrapping it in an Obj-C class. The code here actually consists of several pieces which work together to make using CONREC as versatile as possible. To remind you, what CONREC does is to scan a two-dimensional data set consisting of z (height) values as a function of x and y , that is: f(x,y), and emitting line segments corresponding to specific contour levels within that data set. The contour levels of interest are inputs to CONREC. The original implementation of CONREC consists of a single function with lots of weighty parameters - a precalculated data set to scan, arrays for converting between data indices and actual coordinates, upper and lower bounds, etc. The output handling function is also assumed to exist and linked implicitly.

For our purposes, it is probably easier and more efficient to use CONREC in a different manner. Instead of all those parameters, we encapsulate CONREC in a data processing object, which is supplied two assistant objects - a data source and a data receiver. The processor asks the data source to supply it with various pieces of information on demand, and the data receiver handles the output from CONREC. Both of these assistant objects are declared using an informal protocol, so any suitable object that implements the protocol(s) can be specified.

The key function of the data source is to supply the height value on demand for a given x, y position. The x, y value represents an arbitrary cell within the data set, not necessarily the actual coordinate value. The data source is thus also responsible for mapping the cell x, y, coordinates to some real-valued coordinates as required. Similarly, the actual contour value for a given contour index is also supplied. In this way, CONREC is able to plot contours from arbitrary and irregularly spaced data sets if required. Unlike the original CONREC, the height data doesn't have to be precalculated - it can be done on the fly for each x, y value requested.

The data receiver is simpler: it merely has to process the line segments output by CONREC. The accumulator described in detail below is embodied within a data receiver to convert line segments to vector form as they are generated.

As a further useful convenience for application programmers, a third protocol defines a simple way to hook into CONREC to monitor its progress - depending on the data set CONREC can take a while to run, so running it under a thread and/or keeping the user informed as to how it is getting along are well worth considering.

The code supplied here implements two versions of CONREC. The first version is a straight port adapted to use the datasource/data receiver approach. The algorithm is identical to the original. A second version is also supplied that uses a more optimum algorithm to get better performance. In the original CONREC, each "cell" of the data set is divided into four triangles yielding five vertices (a vertex at the centre of the cell is calculated by averaging the four corners). The four triangles are then used to generate the contour segments where they intersect the notional contour plane. In the modified algorithm, each cell is only divided into two triangles. This means that half the number of triangles are tested, all else being equal, and the centre vertex is not required. Of course this results in a coarser "resolution" for the contours but this is easily compensated for by making the cells themselves smaller, if this is deemed necessary. The second version also has additional optimisations that reduce the number of necessary calls out to the data source. Overall, speedups of 60 - 100% are seen for the modified version over the original given the same data set.

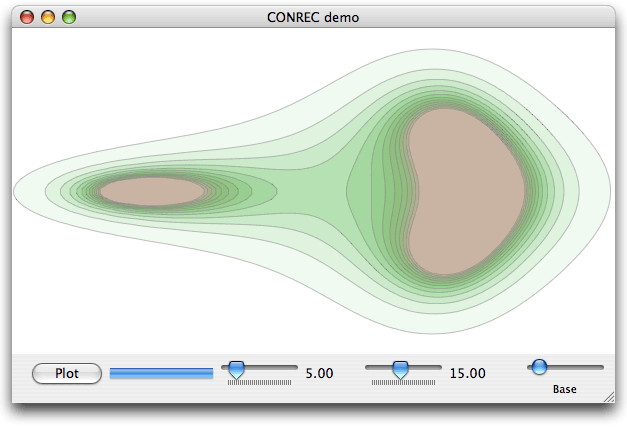
The demo app allows you to interactively adjust a number of parameters - the number of contours, the size of the cells, and the base level and interval of the contours. The height data is generated using the same formula as used for testing in the original BYTE article, so an easy comparison can be made between the original's output and this version's. Unlike the original, the contours are converted to vector (bezier) paths and are stroked and filled to generate the on-screen representation. The rest of this article discusses how this conversion is achieved.

Obtaining output as vector shapes or bezier paths.

In the CONREC algorithm, line segments belonging to a given contour are emitted out of order, because the algorithm scans the data set as an x,y matrix - that is, it doesn't attempt to "follow" contours. For directly drawing these line segments into a pixel buffer, the fact they arrive in some arbitrary order is unimportant. However it will often be preferred that contours can be efficiently converted to a vector form for further processing and drawing - for example as Cocoa developers we might like to treat each contour line as an NSBezierPath object. Sorting an arbitrary collection of unordered line segments (which are known to be at least mostly connected however) is an O(n²) operation, since every line segment needs to be compared against every other line segment to determine if it is connected. No better algorithm for sets of random line segments is known. Clearly such a brute-force approach is going to be very inefficient, and to be avoided. However, contours are not random - by taking advantage of the fact that we know that contours are connected, and sorting as the segments are emitted, substantial efficiency gains should be realised. In fact it's pretty straightforward.

CONREC already knows which contour it is emitting a line segment for, so this is used to initially partition the output data into sets, one per contour. Thus each set need only concern itself with accumulating and matching segments already known to derive from a single contour.

Each element in the data set consists of a list of line segment sequences, stored using a linked list of sequential points. In the worst case, no segment connects to any other, and so the data set consists of separate point pairs (lines). Sorting this set reduces to the brute force method. However, CONREC will not emit such elements, but instead most segments are known to connect to one another eventually.

The data set keeps track of the two end points for each sequence of points. When a new segment is emitted, one of three possibilities exist:

Neither of its end points match the end points of any sequence stored so far
One or other of its end points (but not both) match an end point for a sequence already stored
Both of its end points match end points stored so far

In case (1) there is nothing for it but to simply create a new entry in the data set and store the sequence as a pair of points. As CONREC starts, this will be the most common situation.

In case (2) the new segment may be appended or prepended to an existing sequence, discarding the matched point and only storing the other point that extends the line sequence. The point is appended or prepended to the appropriate sequence. This case will start to occur more frequently as CONREC proceeds and new parts of existing contours are revealed.

In case (3) the new segment is creating a join between two existing line sequences, which thus allows them to be merged into a single sequence. This will occur as separate arms of the same contour converge. For the case of a singly-connected contour, eventually all sequences should become joined and the data set reduces to this single list, which is thus ordered in vector form. From there it is trivial to convert to NSBezierPath, etc.

In order to detect a match, the two new points need to be compared to all of the end points (but only end points) of the current line sequences. As these sequences grow, efficiency improves because only the end points need to be considered and the number of sequences should drop as sequences are merged. Thus the necessary linear search should not end up taking significant time. Only in the case of the segments never matching does the algorithm reduce to the worst-case situation, with a separate sequence stored for every point pair. With CONREC, this should never occur.

Note that the situation of a contour having several disjoint pieces is automatically catered for - such pieces will never be bridged and hence never merged. In addition, cases where a contour arrives at a "pinch point" (a minimum in the data set happens to coincide with the contour level under consideration) should also be handled correctly, creating two disjoint sequences within the same set. This is because as one part of the pinched contour completes, it is merged and thus the "bridge" becomes a segment in the middle of that sequence, and so cannot be matched again. The following bridge for the second part of the pinch point will then work as normal as if the other part were not there.

The accumulator in detail

Data structures are declared that store a single point plus pointers to the next and previous point in the sequence, and to represent each sequence in the complete set. The use of doubly-linked lists helps to keep insertion, deletion and merging operations as efficient as possible, since for typical data sets, CONREC will call this many, many times in the course of its run.

struct Lpt { struct Lpt* next; struct Lpt* prev; Point p; }; typedef struct Lpt Lpt; struct Seq { struct Seq* next; struct Seq* prev; Lpt* head; Lpt* tail; }; typedef struct Seq Seq;

The data set consists simply of the head pointer of the sequence list and optionally a sequence count. The count is incremented for every new sequence added, and decremented for every merge. The count isn't required, but easy to implement and may be useful in some applications. The following C code shows the complete accumulator. The C code has not been directly tested in this form, but is believed to be correct. Note that a generic "Point" type is used here - the Obj-C version uses NSPoint. Also, comparing points for equality as shown here might not always work, due to minor rounding errors. Instead checking that points are "sufficiently close" to be considered equal is a better strategy and is implemented in the 'real' code. Also, it is assumed that the order of each sequence in a disjoint contour is unimportant - the following code orders sequences arbitrarily, the final order depending on numerous factors.

static void reverse_list( Seq* list ); static void remove_seq( Seq* list ); static BOOL points_equal( Point k, Point j ); static Seq* s = NULL; static int count = 0; void conrec_sort( Point a, Point b ) { Seq* ss = s; Seq* ma = NULL; Seq* mb = NULL; BOOL prependA = NO; BOOL prependB = NO; while( ss ) { if ( ma == NULL ) { // no match for a yet if ( points_equal( a, ss->head->p )) { ma = ss; prependA = YES; } else if ( points_equal( a, ss->tail->p )) ma = ss; } if ( mb == NULL ) { // no match for b yet if ( points_equal( b, ss->head->p )) { mb = ss; prependB = YES; } else if ( points_equal( b, ss->tail->p )) mb = ss; } // if we matched both no need to continue searching if ( mb != NULL && ma != NULL ) break; else ss = ss->next; } // c is the case selector based on which of ma and/or mb are set int c = 0; c |= ( ma != NULL )? 1 : 0; c |= ( mb != NULL )? 2 : 0; switch( c ) { case 0: // both unmatched, add as new sequence { Lpt* aa = malloc( sizeof( Lpt )); Lpt* bb = malloc( sizeof( Lpt )); aa->p = a; bb->p = b; aa->next = bb; aa->prev = NULL; bb->prev = aa; bb->next = NULL; // create sequence element and push onto head of main list. The order // of items in this list is unimportant ma = malloc( sizeof( Seq )); ma->head = aa; ma->tail = bb; ma->next = s; ma->prev = NULL; if ( s ) s->prev = ma; s = ma; ++count; // not essential - tracks number of unmerged sequences } break; case 1: // a matched, b did not - thus b extends sequence ma { Lpt* pp = malloc( sizeof( Lpt )); pp->p = b; if ( prependA ) { pp->next = ma->head; pp->prev = NULL; ma->head->prev = pp; ma->head = pp; } else { pp->next = NULL; pp->prev = ma->tail; ma->tail->next = pp; ma->tail = pp; } } break; case 2: // b matched, a did not - thus a extends sequence mb { Lpt* pp = malloc( sizeof( Lpt )); pp->p = a; if ( prependB ) { pp->next = mb->head; pp->prev = NULL; mb->head->prev = pp; mb->head = pp; } else { pp->next = NULL; pp->prev = mb->tail; mb->tail->next = pp; mb->tail = pp; } } break; case 3: // both matched, can merge sequences { // if the sequences are the same, do nothing, as we are simply closing this path (could set a flag) if ( ma == mb ) break; // there are 4 ways the sequence pair can be joined. The current setting of prependA and // prependB will tell us which type of join is needed. For head/head and tail/tail joins // one sequence needs to be reversed int j = 0; j |= prependA? 1 : 0; j |= prependB? 2 : 0; switch( j ) { case 0: // tail-tail // reverse ma and append to mb reverse_list( ma ); // fall through to head/tail case case 1: // head-tail // ma is appended to mb and ma discarded mb->tail->next = ma->head; ma->head->prev = mb->tail; mb->tail = ma->tail; //discard ma sequence record remove_seq( ma ); free( ma ); break; case 3: // head-head // reverse ma and append mb to it reverse_list( ma ); // fall through to tail/head case case 2: // tail-head // mb is appended to ma and mb is discarded ma->tail->next = mb->head; mb->head->prev = ma->tail; ma->tail = mb->tail; //discard mb sequence record remove_seq( mb ); free( mb ); break; } } } } void reverse_list( Seq* list ) { Lpt* pp; Lpt* temp; pp = list->head; while( pp ) { // swap prev/next pointers temp = pp->next; pp->next = pp->prev; pp->prev = temp; // continue through the list pp = temp; } // swap head/tail pointers temp = list->head; list->head = list->tail; list->tail = temp; } void remove_seq( Seq* list ) { // if list is the first item, static ptr s is updated if ( list->prev ) list->prev->next = list->next; else s = list->next; if ( list->next ) list->next->prev = list->prev; --count; } BOOL points_equal( Point k, Point j ) { // implement appropriately, returning YES for a match, NO otherwise return (k.x == j.x) && (k.y == j.y); } void free_seq( Seq* list ) { Lpt* pp = list->head; Lpt* temp; while( pp ) { temp = pp->next; free( pp ); pp = temp; } free( list ); } void free_all() { Seq* ss = s; Seq* temp; while( ss ) { temp = ss->next; free_seq( ss ); ss = temp; } s = NULL; count = 0; }

Once CONREC has completed, each contour will be stored in a readily usable vector form. Converting this to an NSBezierPath represents no great difficulty - we simply walk each sequence and add each point to the path. If the direction of the path along the contour is important, remember that reversing the vector path or the bezier path is very straightforward.